本文经作者同意转载
由于上一次推送的内容有瑕疵,我重新补充了三维下坐标转换的内容,再一次推送。
初学OpenSees时候,可能会对全局坐标和单元局部坐标之间的变换有疑惑,甚至有时候需要大量的例子才能搞明白,本文分享一下自己对这个坐标变换的认识,希望能够帮助到初学者以及向各位学习。若有错误,请批评指正!
其实所谓的坐标转换,其实就是要告诉OpenSees该单元的局部坐标和全局坐标的准确几何变换关系。
#geomTransf Linear transfTag (2维模型)
geomTransf Linear 1
#geomTransf LineartransfTag vecxzXvecxzY $vecxzZ(3维模型)
geomTransf Linear 1 0.000 0.000 1.000
1 全局坐标
1.1 二维
OpenSees建模离不开全局坐标和局部坐标,全局坐标指的是你的结点建模的坐标,例如以下代码就是基于全局坐标建立的4个点坐标,见下图1左。
node 11 0 0;
node 12 6 0;
node 21 0 3;
node 22 6 3;
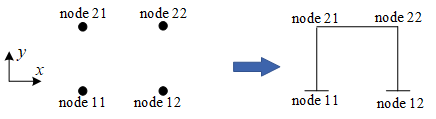
图1 二维全局坐标
1.2 三维
至于三维模型,其z轴方向与x-y轴满足右手定则即可,例如下图2都是可以的,看建模者方便。但是需要注意的是,一旦选了其中一个全局坐标,请记住,这将会影响你后续局部坐标的坐标变换。
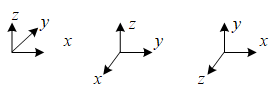
图2 三维全局坐标
2 局部坐标
确定一个具有x-y-z轴的坐标系,由于坐标系方向符合右手定则,只需要确定其中的2个轴的方向即可唯一确定这个坐标系3个方向。
在OpenSees中element的轴向方向为局部坐标的x(已知),接下来只需要确定局部坐标的z方向即可确定该element的局部坐标系(未知)。
因此OpenSees的坐标变换核心就是:告诉OpenSees你的局部坐标系中z轴正方向,其余的计算交给OpenSees。
但用户怎么告诉OpenSees呢?是通过坐标变换向量来完成的,举例如下。
注意:为表示局部与全局坐标的区分,x’和y’代表局部坐标系。
2.1 二维局部坐标变换
如下代码,将node11和node21连起来作为element101,其中node11指向node21为局部坐标系中的x’轴正方向(OpenSees规定)。在二维建模中,局部坐标的z’轴方向默认为指向屏幕外,即在二维建模中局部坐标的x’-z’轴方向已知,从而根据右手定则局部坐标轴x’-y’-z’已知,这也是二维局部坐标变换不需要定义坐标变换向量的原因(geomTransf Linear 1 没有变换向量,但三维模型必须要有变换向量)。
node 11 0 0
...
node 21 0 3
...
geomTransf Linear 1
element nonlinearBeamColumn 101 11 21 npsecID 1;
#npsecID 这两个不需要管,和本次坐标变换不相关
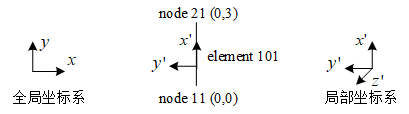
图3 二维模型下全局坐标与局部坐标关系
当确定了element101的局部坐标后,就可以根据其定义你的纤维截面,如下图。

图4 二维模型下的element101纤维截面划分
2.2 三维局部坐标变换
在三维建模中,局部坐标x’方向依旧是element的轴向方向,而局部坐标的z’轴方向不再是指向屏幕外,而是由用户指定一个该向量来确定,该向量(vecxzX,vecxzY,vecxzZ)位于局部坐标系 x’-z’ 平面中,但不重合于x’轴;该向量与x’叉乘得到y’,x’再与y’叉乘得到z’,于是确定了x’-y’-z’。
以下分享一下我在三维建模中遇到两种局部坐标变换的处理方法。
2.2.1 构件轴向方向平行于全局坐标系中的某一轴
node 11 0 0 0
...
node 21 0 3 0
...
set gt1 1
geomTransf Linear gt1 0 0 -1
element nonlinearBeamColumn 101 11 21np secIDgt1;
#npsecID 这两个不需要管,和本次坐标变换不相关
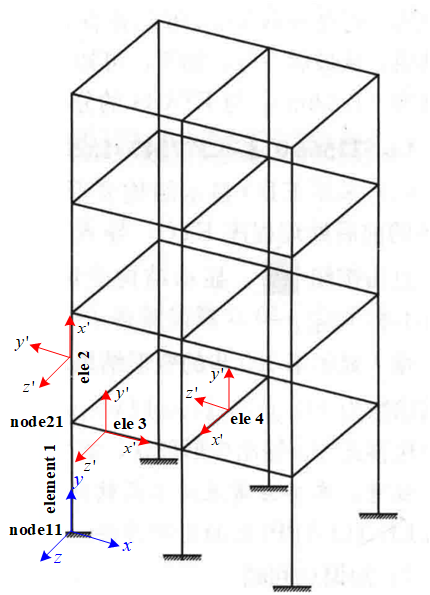
图5 三维建模示意
这个结构所有梁柱的轴向方向x’都与全局坐标系中的某一轴平行。直接旋转全局坐标系的x方向至与梁柱构件的x’方向平行。然后根据旋转后的坐标系中的z’获得坐标变换变量,z’必与全局坐标下的某坐标轴方向平行,例如与y正方向平行,则(vecxzX,vecxzY,vecxzZ)=(0,1,0)。
图5示例:
ele2:(vecxzX,vecxzY,vecxzZ)=(0,0,1)
ele3:(vecxzX,vecxzY,vecxzZ)=(0,0,1)
ele4:(vecxzX,vecxzY,vecxzZ)=(-1,0,0)
2.2.2 构件轴向方向不平行于全局坐标系中的任一轴

图6
如图6所示。
(1)在局部坐标系中指定了一个向量vxz(vecxzX,vecxzY,vecxzZ,用全局坐标来定义的),该向量位于与局部坐标系 x’-z’ 平面平行的平面中,但不重合于x’轴。
(2)向量(vecxzX,vecxzY,vecxzZ)与x’叉乘可以得到y’,而x’和y’叉乘可以得到z’,因此x’-y’-z’均已确定。
然而,上述的vxz定义很清晰,但在三维建模时,每一个单元都的vxz(vecxzX,vecxzY,vecxzZ)应以一定规律地定义,这对后续的数据处理是方便的,其次还可避免一些问题:
下图7所示的梁。如果切换I和J节点但保持vxz不变,局部y轴和z轴会旋转180度。当构件载荷方向是根据局部y’轴定义时,这时候会使该荷载在全局坐标中产生与原定义方向相反的问题,即局部y’轴缺乏不变性。

图7
因此,可以使用以下这个方法来解决这问题:
在局部坐标中的x’-y’平面定义一个变量vxy(注意该变量不能与局部x’轴平行),例如下图8取vxy=(0,1,0)(全局坐标下),局部z’轴可由获得(此局部z’轴可作为vxz),局部y’轴可由获得,这样指定的x’-y’-z’将解决上述图7局部y’轴缺乏不变性的问题。即某轴不变性是通过其定位矢量实现的。
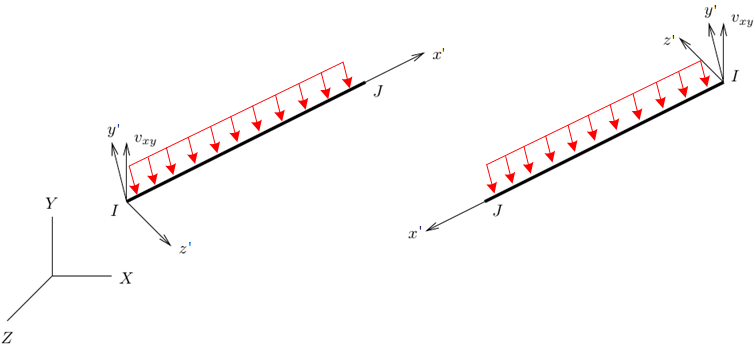
图8
给出Python中结合openseespy来计算图8vxz的代码示例(代码来自Michael H. Scott教授):
# Local x-axis from nodal coordinates
XYZI = ops.nodeCoord(ndI) #获得结点I的X,Y,Z坐标
XYZJ = ops.nodeCoord(ndJ) #获得结点J的X,Y,Z坐标
xaxis = np.subtract(XYZJ,XYZI) #结点J减去结点I坐标以获得局部x'的向量坐标
# Vectors in the local x-y and x-z planes
vecxy = [0,1,0] # 你所定义的vxy坐标(在全局坐标下是垂直向上)
vecxz = np.cross(xaxis,vecxy) # OpenSees中geomTransf所需要的
ops.geomTransf('Linear',1,*vecxz)
2.3 OpenSees的几种坐标变换
OpenSees提供了多种几何坐标变换,例如Linear Transformation、PDelta Transformation、Corotational Transformation(我只认识这几种),用于考虑构件的几何非线性。
Linear Transformation则不考虑几何非线性,用未变形前坐标进行计算;PDelta Transformation可考虑P-delta效应,Corotational Transformation可考虑大位移小应变问题。
#For a two-dimensional problem:
geomTransf Linear transfTag
geomTransf PDeltatransfTag
geomTransf Corotational transfTag
#For a three-dimensional problem:
geomTransf LineartransfTag vecxzXvecxzY vecxzZ
geomTransf PDeltatransfTag vecxzXvecxzY vecxzZ
geomTransf CorotationaltransfTag vecxzXvecxzY $vecxzZ
3 总结
实际上,向量(vecxzX,vecxzY,vecxzZ)可以是任意的(只需要不和x’重合),它不会影响构件在全局坐标下的响应;但当你需要提取局部坐标下的响应时,此时响应的方向则遵循向量(vecxzX,vecxzY,vecxzZ)形成的局部坐标系方向。
